Un physicien de RUDN University a développé un programme pour déterminer la stabilité des trous noirs

Les trous noirs, dont l’existence a été prédite par la théorie générale de la relativité d’Einstein, sont des objets avec une attraction gravitationnelle si forte que même la lumière ne peut pas les quitter. Ces objets denses et massifs déforment l’espace-temps, une structure physique dans laquelle trois dimensions spatiales sont complétées par une quatrième temporelle. De nombreux modèles mathématiques pour décrire les trous noirs incluent des corrections pour affiner cette courbure. Dans ce cas, la condition clé pour tout modèle de trou noir est sa stabilité sous de petits changements dans l’espace-temps. Les trous noirs mathématiquement instables n’ont aucune signification physique : les objets qu’ils décrivent ne peuvent exister. Le physicien de RUDN University a proposé une méthode pour trouver les paramètres auxquels les trous noirs dans l’espace-temps à quatre dimensions seront instables.

"La stabilité d’un trou noir aux petites perturbations de l’espace-temps est une condition nécessaire à la viabilité du modèle considéré. L’une des approches les plus prometteuses pour construire des théories alternatives de la gravité consiste à ajouter des corrections à l’équation d’Einstein. Parmi eux, un rôle important est joué par l’amendement de quatrième ordre Gauss-Bonnet et sa généralisation aux ordres supérieurs, les amendements de Lovelock", Roman Konoplya, chercheur à l’Institut pédagogique et scientifique de gravité et de cosmologie, RUDN University.

Le physicien de RUDN University a étudié la stabilité dans la théorie d’Einstein-Gauss-Bonnet, dans laquelle un trou noir est décrit par l’équation d’Einstein avec un quatrième terme supplémentaire. Auparavant, le physicien avait étudié un problème similaire pour une autre version de la description mathématique des trous noirs : La théorie de Lovelock. Dans celui-ci, un trou noir est décrit en utilisant la somme d’un nombre infini de termes. Il s’est avéré que la région d’instabilité est fermement liée aux valeurs des soi-disant constantes de couplage , les coefficients numériques par lesquels les corrections introduites dans l’équation d’Einstein sont multipliées.

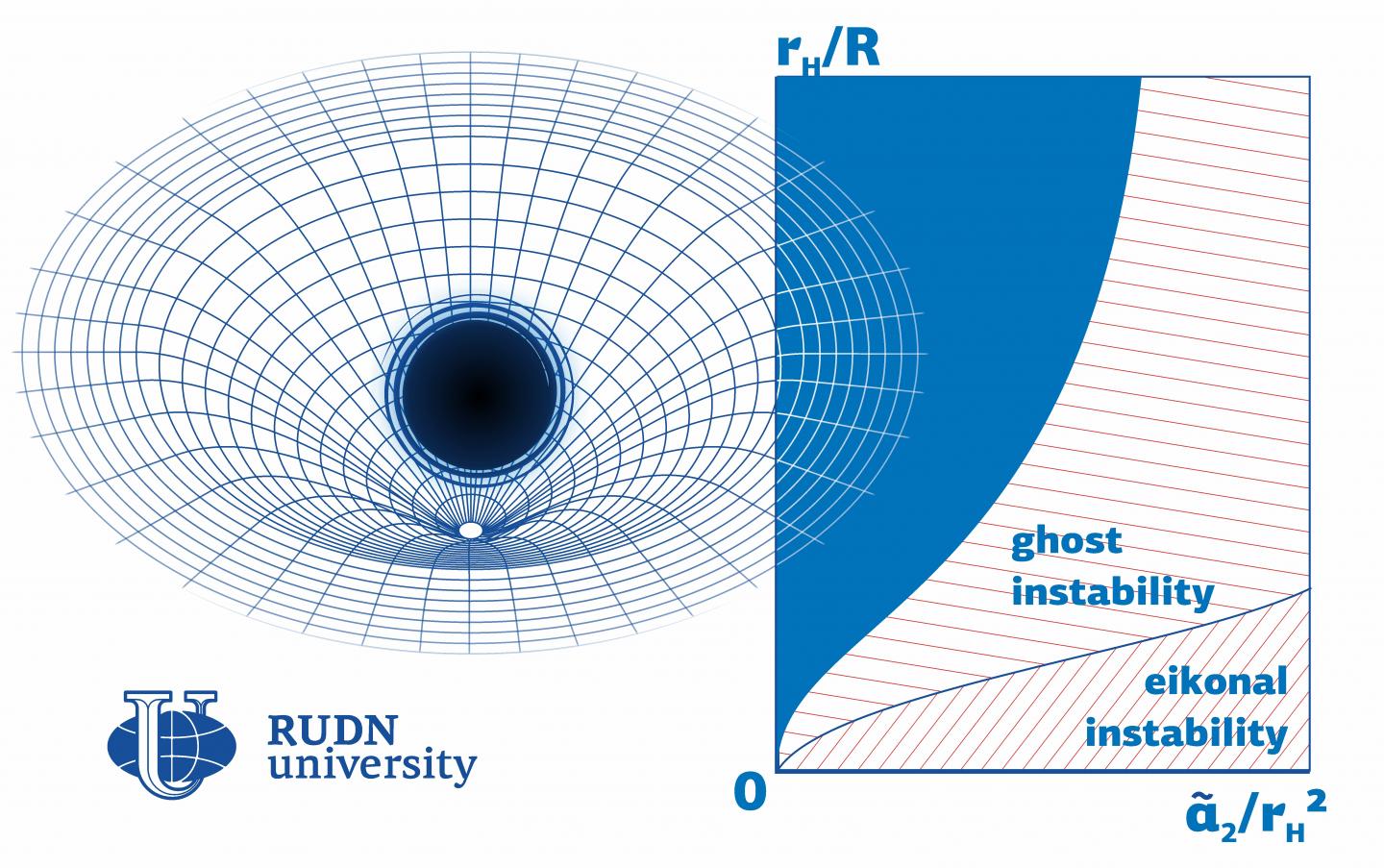
Le physicien de RUDN University a montré que les petits trous noirs ne peuvent pas exister dans le modèle Einstein-Gauss-Bonnet : Si les constantes de couplage sont suffisamment grandes par rapport à d’autres paramètres (par exemple, le rayon d’un trou noir), le modèle est presque toujours instable. Pour des valeurs négatives de la constante de couplage, la région de stabilité est beaucoup plus grande. Sur la base de ces calculs, les physiciens ont créé un code de programme qui vous permet de remplacer n’importe quel paramètre et de calculer si un trou noir avec de tels paramètres sera stable ou non.

"L’approche que nous avons proposée permet de tester la stabilité du modèle de trou noir. Les collègues peuvent utiliser le code que nous avons publié pour construire une région d’instabilité pour des modèles avec un ensemble arbitraire de paramètres" Roman Konoplya, chercheur à l’Institut pédagogique et scientifique de gravité et de cosmologie, RUDN University.

Recherche publiée dans Physics of the Dark Universe