Le mathématicien RUDN a créé un modèle de croissance d'une tumeur cancéreuse

Le nombre de cellules dans une tumeur cancéreuse devrait augmenter de façon exponentielle. Cependant, en réalité, une telle croissance exponentielle n’est observée qu’aux premiers stades du développement de la tumeur. Ensuite, le taux de division diminue. Les principaux facteurs qui affectent cela sont la restriction de l’afflux de nutriments et la contrainte mécanique dans les tissus. Des modèles Mathématiques sont utilisés pour étudier ces processus. Le mathématicien RUDN a proposé un modèle mathématique simple qui prend en compte les principaux facteurs influençant la croissance tumorale.

«La modélisation de la croissance tumorale en tenant compte des propriétés biomécaniques n’est pas un domaine très populaire. L’un des sujets inexplorés est l’influence conjointe de deux facteurs importants qui limitent la croissance tumorale. C’est la disponibilité des nutriments et le stress mécanique», — Maxim Kuznetsov, candidat en sciences physiques et Mathématiques, chercheur associé à l’institut de Mathématiques. S. M. Nikolsky RUDN.

Le modèle qu’il a développé décrit la tumeur et les tissus sains qui l’entourent sous la forme d’une combinaison de solide (le"squelette" des tissus) et de phase liquide (liquide intercellulaire). La phase solide peut apparaître en réduisant la phase liquide — cela correspond à la division des cellules cancéreuses. En revanche, la mort cellulaire correspond à la transition de la phase solide à la phase liquide. Cette dynamique commune mathématicien RUDN décrit à l’aide d’un système d’équations différentielles, puis l’a étudié analytiquement et numériquement.

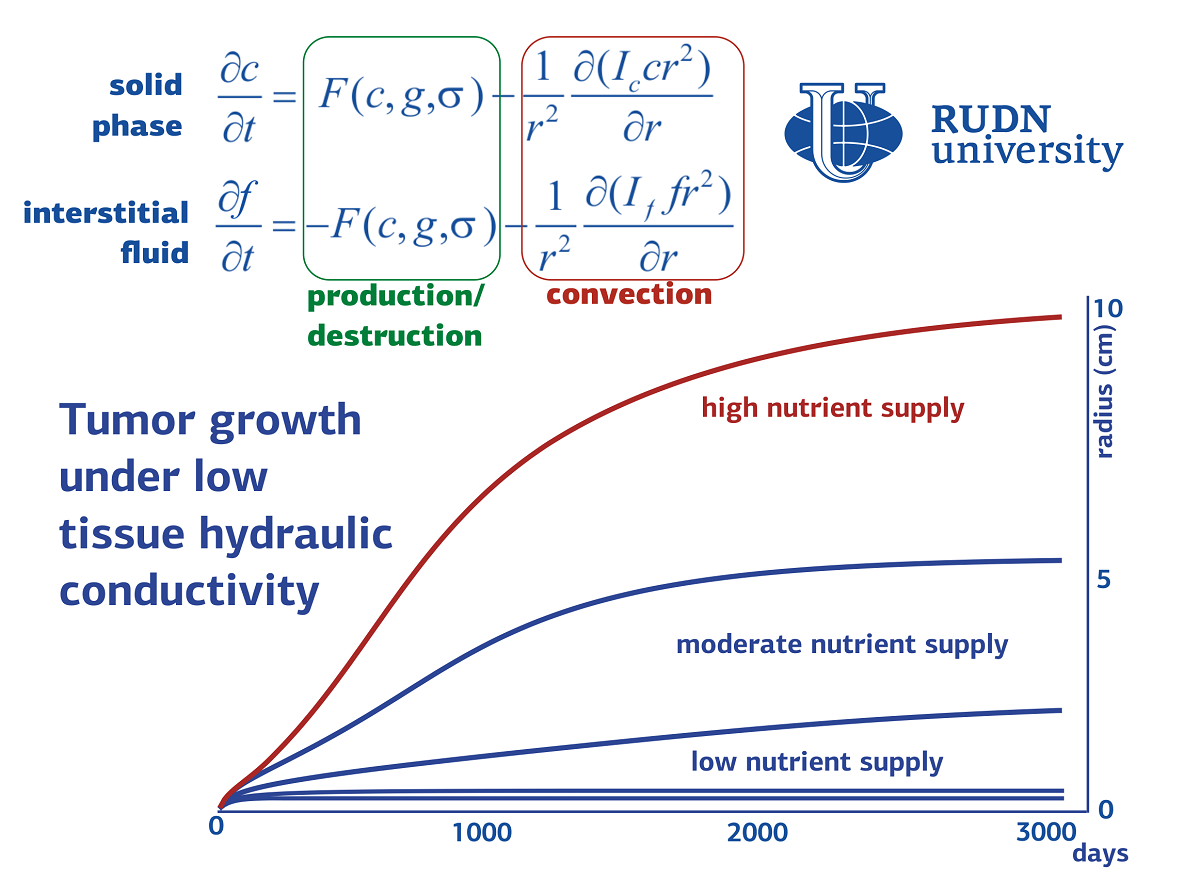
En conséquence, le mathématicien a découvert deux phénomènes. Le premier est la croissance de la tumeur à une taille géante (des dizaines de centimètres de diamètre en quelques années). Dans les calculs numériques, cela s’est produit à un niveau suffisamment élevé d’afflux de nutriments et à une conductivité hydraulique suffisamment faible du tissu — sa capacité à laisser passer le liquide. Fait intéressant, des cas similaires sont décrits dans la pratique clinique réelle. Cela peut arriver avec des tumeurs dont la croissance s’accompagne d’une production abondante de matrice extracellulaire.

Le deuxième phénomène est le ralentissement de la croissance tumorale sous l’action d’une contrainte mécanique à des valeurs minimales de conduction hydraulique. Dans de telles conditions, la croissance tumorale au premier stade ne dépend même pas du niveau d’apport en nutriments. Cependant, en outre, avec un fort afflux de nutriments, une accélération explosive de la croissance d’une tumeur bénigne peut se produire, dans laquelle son taux de croissance peut augmenter des dizaines de fois en quelques années. De tels cas se produisent réellement dans la pratique clinique.

«La principale tâche sur laquelle se concentrera l’étude ultérieure du modèle est l’optimisation grâce à la modélisation mathématique de différents types de traitements tumoraux à long terme associés à l’administration de médicaments à la tumeur par injection intraveineuse. La prise en compte des deux phases du tissu et de la contrainte mécanique qui en résulte reproduira de manière adéquate dans le modèle mathématique la dynamique de l’effet des médicaments sur la tumeur pendant le traitement», a déclaré Maxim Kuznetsov, chercheur associé à l’institut de Mathématiques. S. M. Nikolsky RUDN.

Les résultats sont publiés dans la revue Mathematics.